Red Knight's Shortest Path
Posted on 19 May, 2018 in Algorithm
Hello there, In this post, I will try to analyze Red Knight's Shortest Path problem from HackerRank Before moving on the solution. I would like to explain the vector and queue data structures, that I have used for solving this question. I have used C++ programming language for solving this question.
Vector
We can think vector as an array with more features. It comes with STL library in C++. Here some important information about the vector that we have used for solving this question.
Pushing back(myPreciousVector.push_back(x)) : O(1)
Accessing(myPreciousVector[0]) : O(1)
Queue
The queue is a data structure. We can think it is basically a line. Elements inside the queue are ordered by their push-time. For example, let's assume we have a queue, that contains 1,3,2. That means 1 came earlier than 3 and 2. 3 came earlier than 2. When we push that queue 4. It will go directly to the end(1,3,2,4). When we take from the queue, we will take the element in the front.
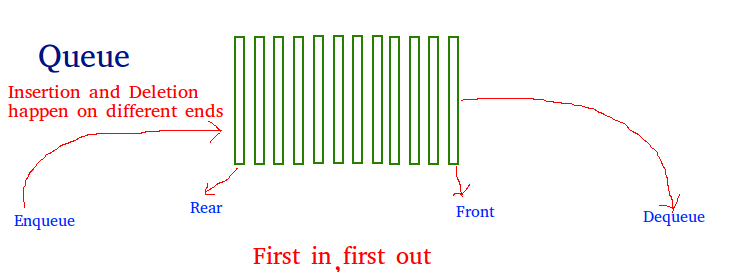
Figure 1: The representation of the queue
When we pop element, we always pop it from the front. When we push element, we always push it to the back. This is the nature of the queue.
Pushing(myPreciousQueue.push(x)) : O(1)
Learning the front element(myPreciousVector.front()) : O(1)
Poping an element(myPreciousVector.pop()) : O(1)
Problem Analysis and Solution
In this problem, we have a starting point, an ending point, and move style. The question asks us to show the path. Therefore, we have to move and store our path. This thought rakes another crucial topic up. It is called Breadth First Search(BFS).
BFS is used for traversing through a graph. The main data structure for BFS is a queue. The main idea for BFS is going to every possible node from the current node one by one. Our graph in this example is chess board. Our edges in chessboard are the nodes that we can reach from the current node.
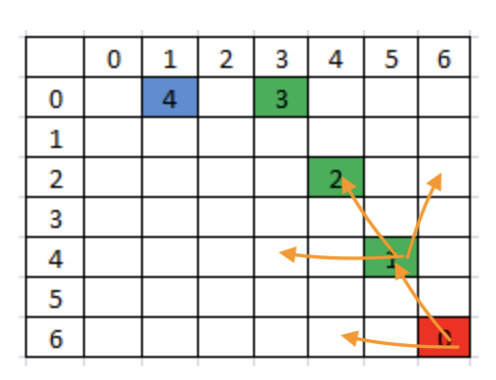
Figure 2: The representation of the BFS Logic
In the figure-2, the red square represents the current location. Therefore, It can follow the orange arrows according to question. After reaching the green square 1, the path is shown in orange arrows. The following code shows the BFS implementation. Before reading the code, be sure that you understood the question.
// Creating a Node struct for representing, where we are in each iteration.
struct Node {
int i{};
int j{};
vector<string> currentPath;
}node;
vector<string> bfs(int iSI, int jSI, const vector<string> ¤tPath, int n, int iE, int jE){
// Creating the main structure queue, and pushing it to our current node.
queue<Node> q;
node.i = iSI, node.j = jSI, node.currentPath = currentPath;
q.push(node);
// Creating visited vector is really critical. We do not want to step that node, that we have been before
vector<vector<int>> visited(static_cast<unsigned long>(n + 4), vector<int>(static_cast<unsigned long>(n + 4), 0));
visited[iSI][jSI] = 0;
// We want to check every node. Therefore, we should loop until q is empty. Remember we are pushing nodes to our queue.
while(!q.empty()){
// Learning the current node
Node currentNode = q.front();
q.pop();
int iS = currentNode.i, jS = currentNode.j;
// If we are in the ending point, return the path.
if(iS == iE && jS == jE)
return currentNode.currentPath;
// We have 6 if statements next for representing the moves, that we can do.
if(iS-2 >= 0 && jS-1 >=0 && visited[iS-2][jS-1] == 0){
// Creating a new node with the current node
Node cNode = currentNode;
cNode.i -= 2;
cNode.j -= 1;
// Saving the path progress
cNode.currentPath.emplace_back("UL");
// Marking the node as visited
visited[iS-2][jS-1] = 1;
// Pushing new node to queue
q.push(cNode);
}
if(iS-2 >= 0 && jS+1 < n && visited[iS-2][jS+1] == 0){
Node cNode = currentNode;
cNode.i -= 2;
cNode.j += 1;
cNode.currentPath.emplace_back("UR");
visited[iS-2][jS+1] = 1;
q.push(cNode);
}
if(jS+2 < n && visited[iS][jS+2] == 0){
Node cNode = currentNode;
cNode.j += 2;
cNode.currentPath.emplace_back("R");
visited[iS][jS+2] = 1;
q.push(cNode);
}
if(iS+2 < n && jS+1 < n && visited[iS+2][jS+1] == 0){
Node cNode = currentNode;
cNode.i += 2;
cNode.j += 1;
cNode.currentPath.emplace_back("LR");
visited[iS+2][jS+1] = 1;
q.push(cNode);
}
if(iS+2 < n && jS-1 >= 0 && visited[iS+2][jS-1] == 0){
Node cNode = currentNode;
cNode.i += 2;
cNode.j -= 1;
cNode.currentPath.emplace_back("LL");
visited[iS+2][jS-1] = 1;
q.push(cNode);
}
if(jS-2 >= 0 && visited[iS][jS-2] == 0){
Node cNode = currentNode;
cNode.j -= 2;
cNode.currentPath.emplace_back("L");
visited[iS][jS-2] = 1;
q.push(cNode);
}
}
return {};
}
// We can think it as the main function.
// We have the starting point, the ending point, and chess board size as inputs
void printShortestPath(int n, int i_start, int j_start, int i_end, int j_end) {
// Running the bfs algorithm and taking the path from it.
vector<string> thePath = bfs(i_start, j_start, {}, n, i_end, j_end);
// If the path is empty, we say there is no path from starting point to ending point.
// If the path is not empty, we print every operation according to the problem.
if(thePath.empty()){
cout << "Impossible" << endl;
}else{
cout << thePath.size() << endl;
for(const auto &i : thePath)
cout << i << " ";
}
}